注意
跳转到末尾下载完整的示例代码。
直方图的箱体、密度和权重#
Axes.hist 方法可以通过几种不同的方式灵活地创建直方图,这种灵活性很有用,但也可能导致混淆。具体来说,你可以
按你希望的方式将数据分箱,无论是通过自动选择的箱体数量,还是通过固定的箱体边缘,
归一化直方图,使其积分值为一,
并为数据点分配权重,使得每个数据点对其所在箱体的计数产生不同的影响。
Matplotlib 的 hist 方法调用 numpy.histogram 并绘制结果,因此用户应查阅 numpy 文档以获取确切指南。
直方图的创建方式是定义箱体边缘,然后将数据集中的值分类到这些箱体中,并计算或汇总每个箱体中有多少数据。在这个简单的例子中,9 个介于 1 和 4 之间的数字被分入 3 个箱体
import matplotlib.pyplot as plt
import numpy as np
rng = np.random.default_rng(19680801)
xdata = np.array([1.2, 2.3, 3.3, 3.1, 1.7, 3.4, 2.1, 1.25, 1.3])
xbins = np.array([1, 2, 3, 4])
# changing the style of the histogram bars just to make it
# very clear where the boundaries of the bins are:
style = {'facecolor': 'none', 'edgecolor': 'C0', 'linewidth': 3}
fig, ax = plt.subplots()
ax.hist(xdata, bins=xbins, **style)
# plot the xdata locations on the x axis:
ax.plot(xdata, 0*xdata, 'd')
ax.set_ylabel('Number per bin')
ax.set_xlabel('x bins (dx=1.0)')
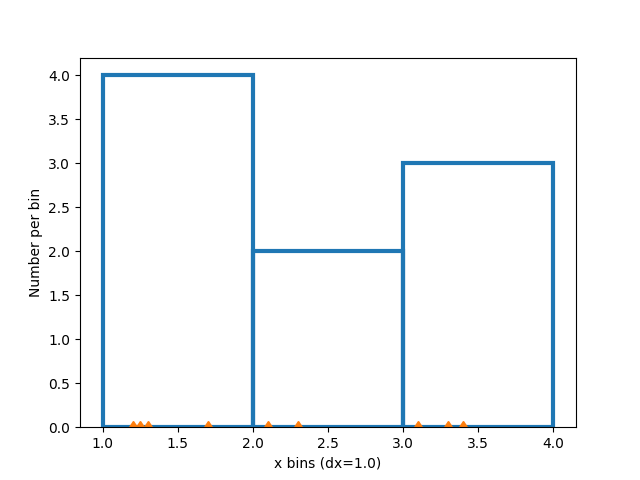
修改箱体#
改变箱体大小会改变这种稀疏直方图的形状,因此,根据你的数据谨慎选择箱体是个好主意。这里我们将箱体宽度减半。
xbins = np.arange(1, 4.5, 0.5)
fig, ax = plt.subplots()
ax.hist(xdata, bins=xbins, **style)
ax.plot(xdata, 0*xdata, 'd')
ax.set_ylabel('Number per bin')
ax.set_xlabel('x bins (dx=0.5)')
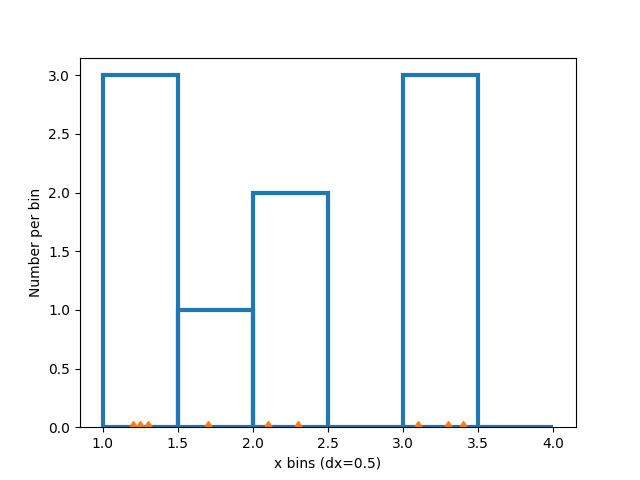
我们也可以让 numpy(通过 Matplotlib)自动选择箱体,或指定一个数量让其自动选择箱体
fig, ax = plt.subplot_mosaic([['auto', 'n4']],
sharex=True, sharey=True, layout='constrained')
ax['auto'].hist(xdata, **style)
ax['auto'].plot(xdata, 0*xdata, 'd')
ax['auto'].set_ylabel('Number per bin')
ax['auto'].set_xlabel('x bins (auto)')
ax['n4'].hist(xdata, bins=4, **style)
ax['n4'].plot(xdata, 0*xdata, 'd')
ax['n4'].set_xlabel('x bins ("bins=4")')
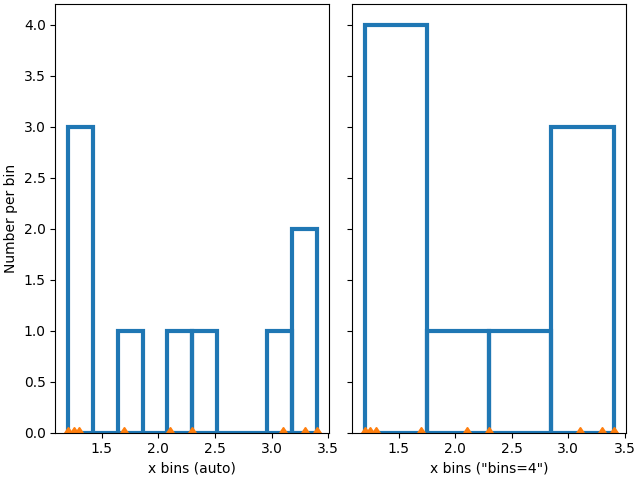
直方图归一化:密度和权重#
每个箱体的计数是直方图中每个条形的默认长度。但是,我们也可以使用 density 参数将条形长度归一化为概率密度函数
fig, ax = plt.subplots()
ax.hist(xdata, bins=xbins, density=True, **style)
ax.set_ylabel('Probability density [$V^{-1}$])')
ax.set_xlabel('x bins (dx=0.5 $V$)')
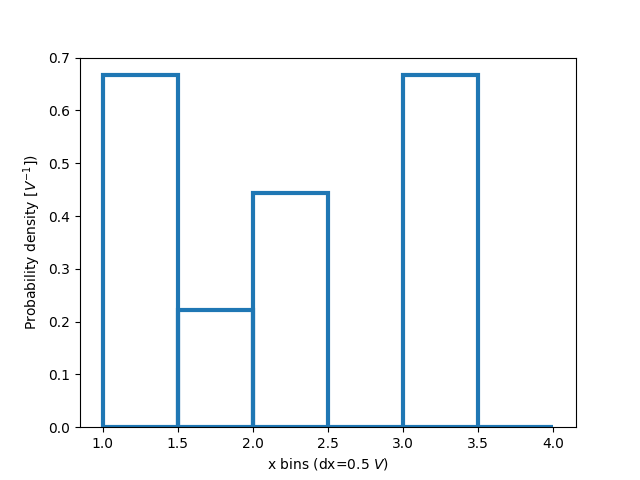
这种归一化在仅探索数据时可能有点难以解释。每个条形上的值被总数据点数和箱体宽度除以,因此,当对数据的整个范围进行积分时,这些值会积分到一。例如,
density = counts / (sum(counts) * np.diff(bins))
np.sum(density * np.diff(bins)) == 1
这种归一化是统计学中定义概率密度函数的方式。如果 \(X\) 是 \(x\) 上的随机变量,那么如果 \(P[a<X<b] = \int_a^b f_X dx\),则 \(f_X\) 是概率密度函数。如果 x 的单位是伏特,那么 \(f_X\) 的单位是 \(V^{-1}\) 或每伏特变化的概率。
当我们从已知分布中抽取并尝试与理论进行比较时,这种归一化的用处会更清楚一些。因此,从正态分布中选择 1000 个点,并计算已知的概率密度函数
如果我们不使用 density=True,我们需要将预期的概率分布函数按数据长度和箱体宽度进行缩放
fig, ax = plt.subplot_mosaic([['False', 'True']], layout='constrained')
dx = 0.1
xbins = np.arange(-4, 4, dx)
ax['False'].hist(xdata, bins=xbins, density=False, histtype='step', label='Counts')
# scale and plot the expected pdf:
ax['False'].plot(xpdf, pdf * len(xdata) * dx, label=r'$N\,f_X(x)\,\delta x$')
ax['False'].set_ylabel('Count per bin')
ax['False'].set_xlabel('x bins [V]')
ax['False'].legend()
ax['True'].hist(xdata, bins=xbins, density=True, histtype='step', label='density')
ax['True'].plot(xpdf, pdf, label='$f_X(x)$')
ax['True'].set_ylabel('Probability density [$V^{-1}$]')
ax['True'].set_xlabel('x bins [$V$]')
ax['True'].legend()
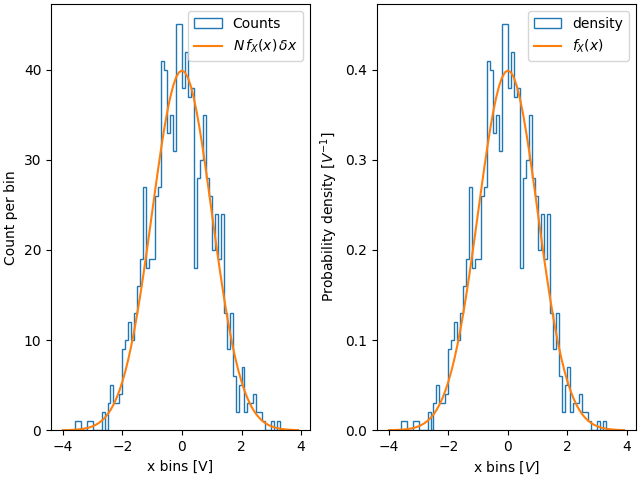
因此,使用密度的优点是直方图的形状和振幅不取决于箱体的大小。考虑一个极端情况,即箱体宽度不同。在此示例中,x=-1.25 以下的箱体宽度是其余箱体的六倍。通过按密度归一化,我们保留了分布的形状,而如果不这样做,则较宽的箱体将比窄箱体具有更高的计数
fig, ax = plt.subplot_mosaic([['False', 'True']], layout='constrained')
dx = 0.1
xbins = np.hstack([np.arange(-4, -1.25, 6*dx), np.arange(-1.25, 4, dx)])
ax['False'].hist(xdata, bins=xbins, density=False, histtype='step', label='Counts')
ax['False'].plot(xpdf, pdf * len(xdata) * dx, label=r'$N\,f_X(x)\,\delta x_0$')
ax['False'].set_ylabel('Count per bin')
ax['False'].set_xlabel('x bins [V]')
ax['False'].legend()
ax['True'].hist(xdata, bins=xbins, density=True, histtype='step', label='density')
ax['True'].plot(xpdf, pdf, label='$f_X(x)$')
ax['True'].set_ylabel('Probability density [$V^{-1}$]')
ax['True'].set_xlabel('x bins [$V$]')
ax['True'].legend()
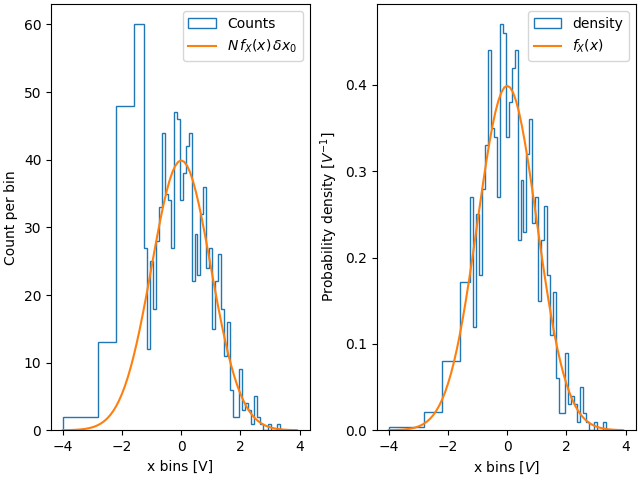
同样,如果我们要比较具有不同箱体宽度的直方图,我们可能需要使用 density=True
fig, ax = plt.subplot_mosaic([['False', 'True']], layout='constrained')
# expected PDF
ax['True'].plot(xpdf, pdf, '--', label='$f_X(x)$', color='k')
for nn, dx in enumerate([0.1, 0.4, 1.2]):
xbins = np.arange(-4, 4, dx)
# expected histogram:
ax['False'].plot(xpdf, pdf*1000*dx, '--', color=f'C{nn}')
ax['False'].hist(xdata, bins=xbins, density=False, histtype='step')
ax['True'].hist(xdata, bins=xbins, density=True, histtype='step', label=dx)
# Labels:
ax['False'].set_xlabel('x bins [$V$]')
ax['False'].set_ylabel('Count per bin')
ax['True'].set_ylabel('Probability density [$V^{-1}$]')
ax['True'].set_xlabel('x bins [$V$]')
ax['True'].legend(fontsize='small', title='bin width:')
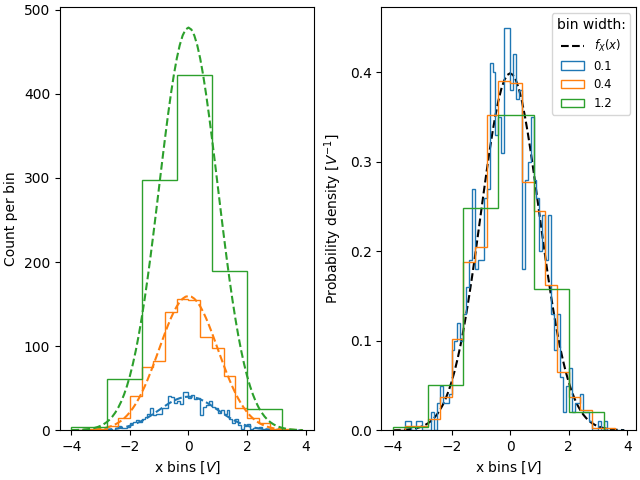
有时人们希望进行归一化,使得计数的总和为一。这类似于离散变量的概率质量函数,其中所有值的概率之和等于一。使用 hist,如果我们将权重设置为 1/N,就可以实现这种归一化。请注意,这种归一化直方图的振幅仍然取决于箱体的宽度和/或数量
fig, ax = plt.subplots(layout='constrained', figsize=(3.5, 3))
for nn, dx in enumerate([0.1, 0.4, 1.2]):
xbins = np.arange(-4, 4, dx)
ax.hist(xdata, bins=xbins, weights=1/len(xdata) * np.ones(len(xdata)),
histtype='step', label=f'{dx}')
ax.set_xlabel('x bins [$V$]')
ax.set_ylabel('Bin count / N')
ax.legend(fontsize='small', title='bin width:')
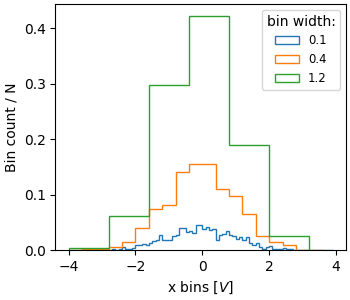
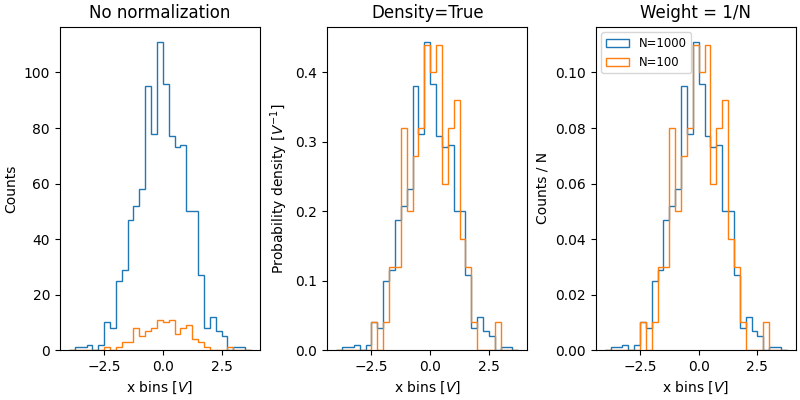
归一化直方图的价值在于比较具有不同群体大小的两个分布。这里我们比较 `xdata`(1000 个成员)和 `xdata2`(100 个成员)的分布。
xdata2 = rng.normal(size=100)
fig, ax = plt.subplot_mosaic([['no_norm', 'density', 'weight']],
layout='constrained', figsize=(8, 4))
xbins = np.arange(-4, 4, 0.25)
ax['no_norm'].hist(xdata, bins=xbins, histtype='step')
ax['no_norm'].hist(xdata2, bins=xbins, histtype='step')
ax['no_norm'].set_ylabel('Counts')
ax['no_norm'].set_xlabel('x bins [$V$]')
ax['no_norm'].set_title('No normalization')
ax['density'].hist(xdata, bins=xbins, histtype='step', density=True)
ax['density'].hist(xdata2, bins=xbins, histtype='step', density=True)
ax['density'].set_ylabel('Probability density [$V^{-1}$]')
ax['density'].set_title('Density=True')
ax['density'].set_xlabel('x bins [$V$]')
ax['weight'].hist(xdata, bins=xbins, histtype='step',
weights=1 / len(xdata) * np.ones(len(xdata)),
label='N=1000')
ax['weight'].hist(xdata2, bins=xbins, histtype='step',
weights=1 / len(xdata2) * np.ones(len(xdata2)),
label='N=100')
ax['weight'].set_xlabel('x bins [$V$]')
ax['weight'].set_ylabel('Counts / N')
ax['weight'].legend(fontsize='small')
ax['weight'].set_title('Weight = 1/N')
plt.show()
参考
本示例展示了以下函数、方法、类和模块的使用
脚本总运行时间: (0 分 5.244 秒)