注意
前往末尾以下载完整示例代码。
绘制二维数据集的置信椭圆#
此示例展示了如何使用皮尔逊相关系数绘制二维数据集的置信椭圆。
获取正确几何形状的方法在此处进行了说明和证明
https://carstenschelp.github.io/2018/09/14/Plot_Confidence_Ellipse_001.html
该方法避免了使用迭代特征分解算法,并利用了归一化协方差矩阵(由皮尔逊相关系数和单位组成)特别易于处理的特点。
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.patches import Ellipse
import matplotlib.transforms as transforms
绘图函数本身#
此函数绘制给定数组型变量 x 和 y 的协方差的置信椭圆。椭圆绘制到给定的 Axes 对象 ax 中。
椭圆的半径可以通过 n_std 控制,n_std 是标准差的数量。默认值为 3,如果数据像这些示例中一样呈正态分布,则使椭圆包含 98.9% 的点(1D 中的 3 个标准差包含 99.7% 的数据,即 2D 中 98.9% 的数据)。
def confidence_ellipse(x, y, ax, n_std=3.0, facecolor='none', **kwargs):
"""
Create a plot of the covariance confidence ellipse of *x* and *y*.
Parameters
----------
x, y : array-like, shape (n, )
Input data.
ax : matplotlib.axes.Axes
The Axes object to draw the ellipse into.
n_std : float
The number of standard deviations to determine the ellipse's radiuses.
**kwargs
Forwarded to `~matplotlib.patches.Ellipse`
Returns
-------
matplotlib.patches.Ellipse
"""
if x.size != y.size:
raise ValueError("x and y must be the same size")
cov = np.cov(x, y)
pearson = cov[0, 1]/np.sqrt(cov[0, 0] * cov[1, 1])
# Using a special case to obtain the eigenvalues of this
# two-dimensional dataset.
ell_radius_x = np.sqrt(1 + pearson)
ell_radius_y = np.sqrt(1 - pearson)
ellipse = Ellipse((0, 0), width=ell_radius_x * 2, height=ell_radius_y * 2,
facecolor=facecolor, **kwargs)
# Calculating the standard deviation of x from
# the squareroot of the variance and multiplying
# with the given number of standard deviations.
scale_x = np.sqrt(cov[0, 0]) * n_std
mean_x = np.mean(x)
# calculating the standard deviation of y ...
scale_y = np.sqrt(cov[1, 1]) * n_std
mean_y = np.mean(y)
transf = transforms.Affine2D() \
.rotate_deg(45) \
.scale(scale_x, scale_y) \
.translate(mean_x, mean_y)
ellipse.set_transform(transf + ax.transData)
return ax.add_patch(ellipse)
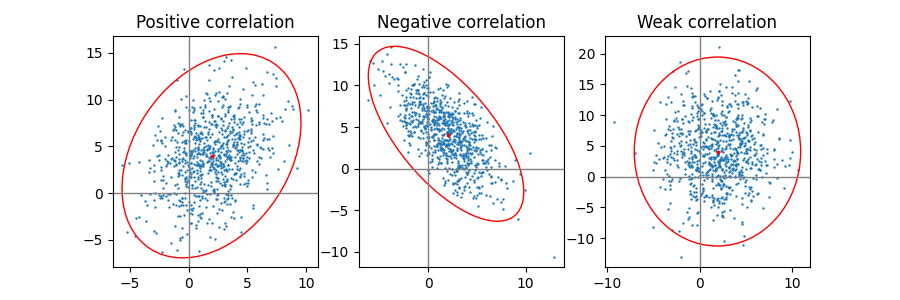
正相关、负相关和弱相关#
请注意,弱相关(右侧)的形状是椭圆而不是圆形,因为 x 和 y 的比例不同。然而,椭圆的轴与坐标系的 x 轴和 y 轴对齐,这表明 x 和 y 是不相关的。
np.random.seed(0)
PARAMETERS = {
'Positive correlation': [[0.85, 0.35],
[0.15, -0.65]],
'Negative correlation': [[0.9, -0.4],
[0.1, -0.6]],
'Weak correlation': [[1, 0],
[0, 1]],
}
mu = 2, 4
scale = 3, 5
fig, axs = plt.subplots(1, 3, figsize=(9, 3))
for ax, (title, dependency) in zip(axs, PARAMETERS.items()):
x, y = get_correlated_dataset(800, dependency, mu, scale)
ax.scatter(x, y, s=0.5)
ax.axvline(c='grey', lw=1)
ax.axhline(c='grey', lw=1)
confidence_ellipse(x, y, ax, edgecolor='red')
ax.scatter(mu[0], mu[1], c='red', s=3)
ax.set_title(title)
plt.show()
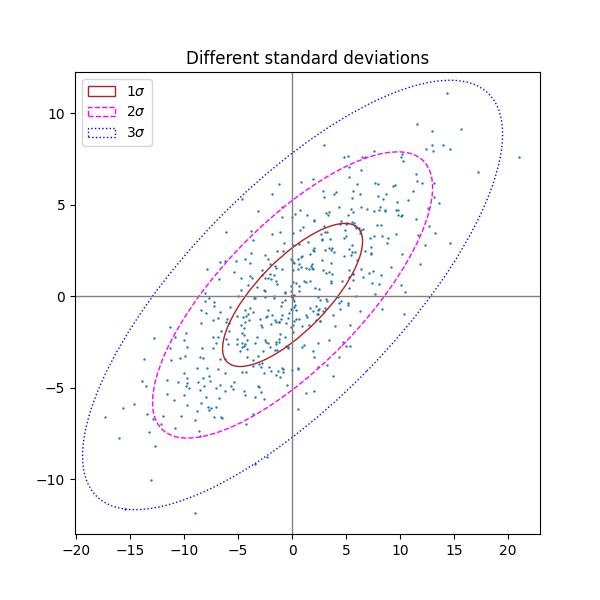
不同数量的标准差#
一个 n_std = 3(蓝色)、2(紫色)和 1(红色)的图
fig, ax_nstd = plt.subplots(figsize=(6, 6))
dependency_nstd = [[0.8, 0.75],
[-0.2, 0.35]]
mu = 0, 0
scale = 8, 5
ax_nstd.axvline(c='grey', lw=1)
ax_nstd.axhline(c='grey', lw=1)
x, y = get_correlated_dataset(500, dependency_nstd, mu, scale)
ax_nstd.scatter(x, y, s=0.5)
confidence_ellipse(x, y, ax_nstd, n_std=1,
label=r'$1\sigma$', edgecolor='firebrick')
confidence_ellipse(x, y, ax_nstd, n_std=2,
label=r'$2\sigma$', edgecolor='fuchsia', linestyle='--')
confidence_ellipse(x, y, ax_nstd, n_std=3,
label=r'$3\sigma$', edgecolor='blue', linestyle=':')
ax_nstd.scatter(mu[0], mu[1], c='red', s=3)
ax_nstd.set_title('Different standard deviations')
ax_nstd.legend()
plt.show()
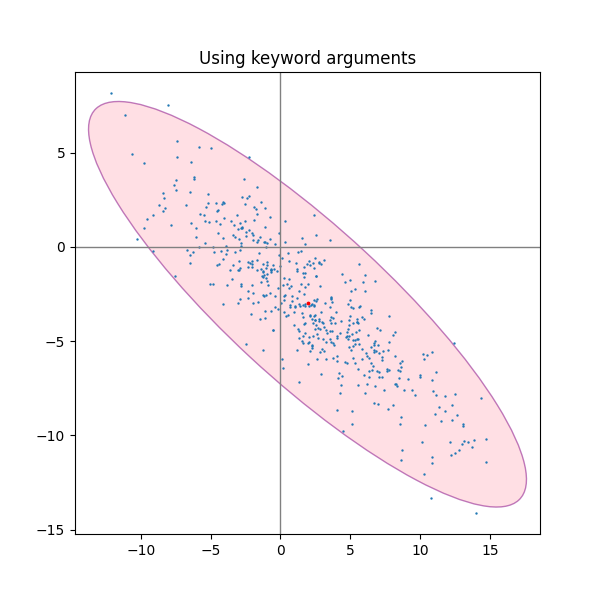
使用关键字参数#
使用为 matplotlib.patches.Patch 指定的关键字参数,以便以不同方式渲染椭圆。
fig, ax_kwargs = plt.subplots(figsize=(6, 6))
dependency_kwargs = [[-0.8, 0.5],
[-0.2, 0.5]]
mu = 2, -3
scale = 6, 5
ax_kwargs.axvline(c='grey', lw=1)
ax_kwargs.axhline(c='grey', lw=1)
x, y = get_correlated_dataset(500, dependency_kwargs, mu, scale)
# Plot the ellipse with zorder=0 in order to demonstrate
# its transparency (caused by the use of alpha).
confidence_ellipse(x, y, ax_kwargs,
alpha=0.5, facecolor='pink', edgecolor='purple', zorder=0)
ax_kwargs.scatter(x, y, s=0.5)
ax_kwargs.scatter(mu[0], mu[1], c='red', s=3)
ax_kwargs.set_title('Using keyword arguments')
fig.subplots_adjust(hspace=0.25)
plt.show()
脚本总运行时间: (0 分钟 2.882 秒)