注意
跳转到末尾 以下载完整示例代码。
Asinh 刻度#
asinh 轴缩放的示例,其使用以下变换
\[a \rightarrow a_0 \sinh^{-1} (a / a_0)\]
对于接近零的坐标值(即远小于“线性宽度” \(a_0\)),这使得值基本保持不变
\[a \rightarrow a + \mathcal{O}(a^3)\]
但对于较大的值(即 \(|a| \gg a_0\)),这渐近地为
\[a \rightarrow a_0 \, \mathrm{sgn}(a) \ln |a| + \mathcal{O}(1)\]
与 symlog 缩放一样,这允许绘制覆盖非常宽的动态范围(包括正值和负值)的量。然而,symlog 涉及的变换在其梯度中存在不连续性,因为它是由单独的线性和对数变换构建的。asinh 缩放使用的变换对于所有(有限)值都是平滑的,这在数学上更简洁,并减少了与图中线性和对数区域之间突然过渡相关的视觉伪影。
注意
scale.AsinhScale 尚处于实验阶段,且其 API 可能会发生变化。
参见 AsinhScale,SymmetricalLogScale。
import matplotlib.pyplot as plt
import numpy as np
# Prepare sample values for variations on y=x graph:
x = np.linspace(-3, 6, 500)
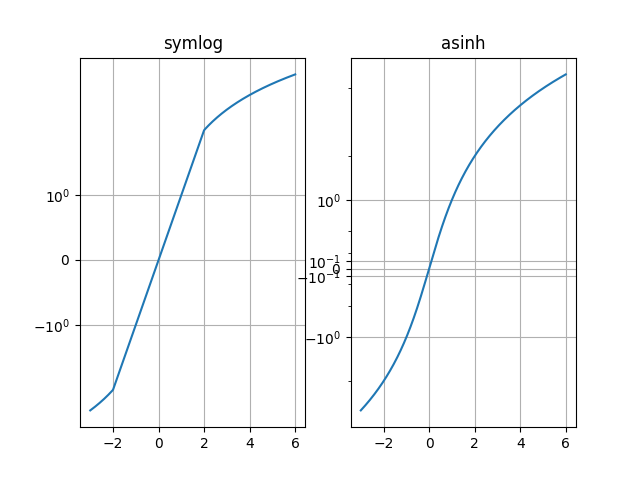
比较 "symlog" 和 "asinh" 在示例 y=x 图上的行为,其中 "symlog" 在 y=2 附近存在不连续梯度
fig1 = plt.figure()
ax0, ax1 = fig1.subplots(1, 2, sharex=True)
ax0.plot(x, x)
ax0.set_yscale('symlog')
ax0.grid()
ax0.set_title('symlog')
ax1.plot(x, x)
ax1.set_yscale('asinh')
ax1.grid()
ax1.set_title('asinh')
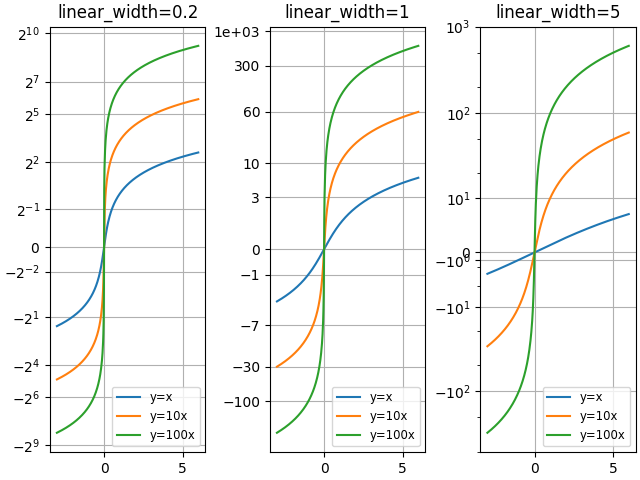
比较具有不同刻度参数“linear_width”的“asinh”图
fig2 = plt.figure(layout='constrained')
axs = fig2.subplots(1, 3, sharex=True)
for ax, (a0, base) in zip(axs, ((0.2, 2), (1.0, 0), (5.0, 10))):
ax.set_title(f'linear_width={a0:.3g}')
ax.plot(x, x, label='y=x')
ax.plot(x, 10*x, label='y=10x')
ax.plot(x, 100*x, label='y=100x')
ax.set_yscale('asinh', linear_width=a0, base=base)
ax.grid()
ax.legend(loc='best', fontsize='small')
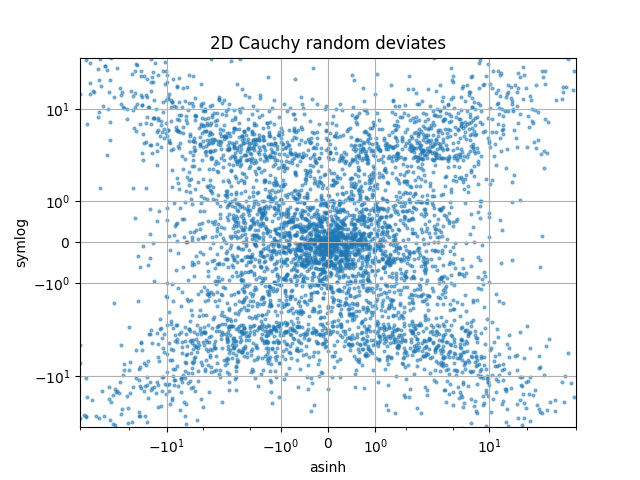
比较 "symlog" 和 "asinh" 缩放,在二维柯西分布随机数上的表现,其中在 y=2 附近可能会看到更细微的伪影,这是由于 "symlog" 中的梯度不连续性所致。
fig3 = plt.figure()
ax = fig3.subplots(1, 1)
r = 3 * np.tan(np.random.uniform(-np.pi / 2.02, np.pi / 2.02,
size=(5000,)))
th = np.random.uniform(0, 2*np.pi, size=r.shape)
ax.scatter(r * np.cos(th), r * np.sin(th), s=4, alpha=0.5)
ax.set_xscale('asinh')
ax.set_yscale('symlog')
ax.set_xlabel('asinh')
ax.set_ylabel('symlog')
ax.set_title('2D Cauchy random deviates')
ax.set_xlim(-50, 50)
ax.set_ylim(-50, 50)
ax.grid()
plt.show()
脚本总运行时间: (0 分钟 2.584 秒)