注意
跳转到末尾以下载完整的示例代码。
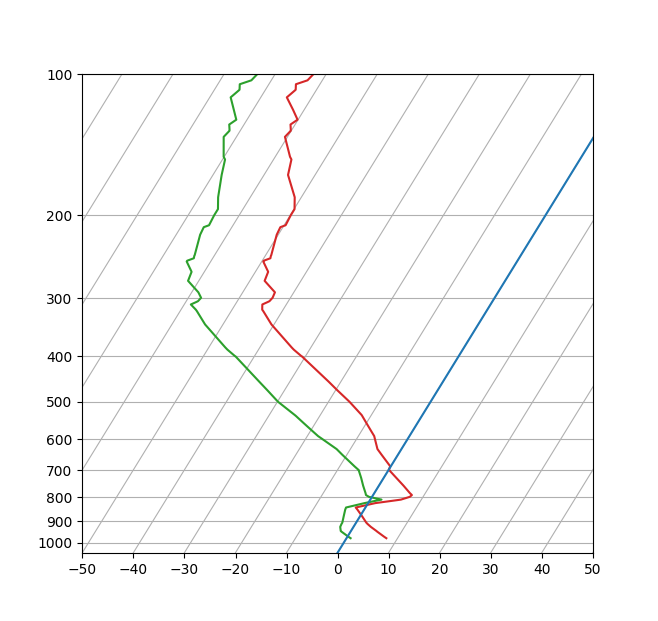
SkewT-logP 图:使用变换和自定义投影#
这是对 Matplotlib 变换和自定义投影 API 的一项深入练习。本示例生成了一个所谓的 SkewT-logP 图,这是气象学中用于显示温度垂直廓线的常用图表。就 Matplotlib 而言,其复杂性在于 X 轴和 Y 轴并非正交。这通过在基本 Axes 变换中引入一个倾斜(skew)分量来解决。额外的复杂性在于处理上下 X 轴具有不同数据范围的事实,这需要一堆自定义的刻度、边界和轴类来处理。
from contextlib import ExitStack
from matplotlib.axes import Axes
import matplotlib.axis as maxis
from matplotlib.projections import register_projection
import matplotlib.spines as mspines
import matplotlib.transforms as transforms
# The sole purpose of this class is to look at the upper, lower, or total
# interval as appropriate and see what parts of the tick to draw, if any.
class SkewXTick(maxis.XTick):
def draw(self, renderer):
# When adding the callbacks with `stack.callback`, we fetch the current
# visibility state of the artist with `get_visible`; the ExitStack will
# restore these states (`set_visible`) at the end of the block (after
# the draw).
with ExitStack() as stack:
for artist in [self.gridline, self.tick1line, self.tick2line,
self.label1, self.label2]:
stack.callback(artist.set_visible, artist.get_visible())
needs_lower = transforms.interval_contains(
self.axes.lower_xlim, self.get_loc())
needs_upper = transforms.interval_contains(
self.axes.upper_xlim, self.get_loc())
self.tick1line.set_visible(
self.tick1line.get_visible() and needs_lower)
self.label1.set_visible(
self.label1.get_visible() and needs_lower)
self.tick2line.set_visible(
self.tick2line.get_visible() and needs_upper)
self.label2.set_visible(
self.label2.get_visible() and needs_upper)
super().draw(renderer)
def get_view_interval(self):
return self.axes.xaxis.get_view_interval()
# This class exists to provide two separate sets of intervals to the tick,
# as well as create instances of the custom tick
class SkewXAxis(maxis.XAxis):
def _get_tick(self, major):
return SkewXTick(self.axes, None, major=major)
def get_view_interval(self):
return self.axes.upper_xlim[0], self.axes.lower_xlim[1]
# This class exists to calculate the separate data range of the
# upper X-axis and draw the spine there. It also provides this range
# to the X-axis artist for ticking and gridlines
class SkewSpine(mspines.Spine):
def _adjust_location(self):
pts = self._path.vertices
if self.spine_type == 'top':
pts[:, 0] = self.axes.upper_xlim
else:
pts[:, 0] = self.axes.lower_xlim
# This class handles registration of the skew-xaxes as a projection as well
# as setting up the appropriate transformations. It also overrides standard
# spines and axes instances as appropriate.
class SkewXAxes(Axes):
# The projection must specify a name. This will be used be the
# user to select the projection, i.e. ``subplot(projection='skewx')``.
name = 'skewx'
def _init_axis(self):
# Taken from Axes and modified to use our modified X-axis
self.xaxis = SkewXAxis(self)
self.spines.top.register_axis(self.xaxis)
self.spines.bottom.register_axis(self.xaxis)
self.yaxis = maxis.YAxis(self)
self.spines.left.register_axis(self.yaxis)
self.spines.right.register_axis(self.yaxis)
def _gen_axes_spines(self):
spines = {'top': SkewSpine.linear_spine(self, 'top'),
'bottom': mspines.Spine.linear_spine(self, 'bottom'),
'left': mspines.Spine.linear_spine(self, 'left'),
'right': mspines.Spine.linear_spine(self, 'right')}
return spines
def _set_lim_and_transforms(self):
"""
This is called once when the plot is created to set up all the
transforms for the data, text and grids.
"""
rot = 30
# Get the standard transform setup from the Axes base class
super()._set_lim_and_transforms()
# Need to put the skew in the middle, after the scale and limits,
# but before the transAxes. This way, the skew is done in Axes
# coordinates thus performing the transform around the proper origin
# We keep the pre-transAxes transform around for other users, like the
# spines for finding bounds
self.transDataToAxes = (
self.transScale
+ self.transLimits
+ transforms.Affine2D().skew_deg(rot, 0)
)
# Create the full transform from Data to Pixels
self.transData = self.transDataToAxes + self.transAxes
# Blended transforms like this need to have the skewing applied using
# both axes, in axes coords like before.
self._xaxis_transform = (
transforms.blended_transform_factory(
self.transScale + self.transLimits,
transforms.IdentityTransform())
+ transforms.Affine2D().skew_deg(rot, 0)
+ self.transAxes
)
@property
def lower_xlim(self):
return self.axes.viewLim.intervalx
@property
def upper_xlim(self):
pts = [[0., 1.], [1., 1.]]
return self.transDataToAxes.inverted().transform(pts)[:, 0]
# Now register the projection with matplotlib so the user can select it.
register_projection(SkewXAxes)
if __name__ == '__main__':
# Now make a simple example using the custom projection.
from io import StringIO
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.ticker import (MultipleLocator, NullFormatter,
ScalarFormatter)
# Some example data.
data_txt = '''
978.0 345 7.8 0.8
971.0 404 7.2 0.2
946.7 610 5.2 -1.8
944.0 634 5.0 -2.0
925.0 798 3.4 -2.6
911.8 914 2.4 -2.7
906.0 966 2.0 -2.7
877.9 1219 0.4 -3.2
850.0 1478 -1.3 -3.7
841.0 1563 -1.9 -3.8
823.0 1736 1.4 -0.7
813.6 1829 4.5 1.2
809.0 1875 6.0 2.2
798.0 1988 7.4 -0.6
791.0 2061 7.6 -1.4
783.9 2134 7.0 -1.7
755.1 2438 4.8 -3.1
727.3 2743 2.5 -4.4
700.5 3048 0.2 -5.8
700.0 3054 0.2 -5.8
698.0 3077 0.0 -6.0
687.0 3204 -0.1 -7.1
648.9 3658 -3.2 -10.9
631.0 3881 -4.7 -12.7
600.7 4267 -6.4 -16.7
592.0 4381 -6.9 -17.9
577.6 4572 -8.1 -19.6
555.3 4877 -10.0 -22.3
536.0 5151 -11.7 -24.7
533.8 5182 -11.9 -25.0
500.0 5680 -15.9 -29.9
472.3 6096 -19.7 -33.4
453.0 6401 -22.4 -36.0
400.0 7310 -30.7 -43.7
399.7 7315 -30.8 -43.8
387.0 7543 -33.1 -46.1
382.7 7620 -33.8 -46.8
342.0 8398 -40.5 -53.5
320.4 8839 -43.7 -56.7
318.0 8890 -44.1 -57.1
310.0 9060 -44.7 -58.7
306.1 9144 -43.9 -57.9
305.0 9169 -43.7 -57.7
300.0 9280 -43.5 -57.5
292.0 9462 -43.7 -58.7
276.0 9838 -47.1 -62.1
264.0 10132 -47.5 -62.5
251.0 10464 -49.7 -64.7
250.0 10490 -49.7 -64.7
247.0 10569 -48.7 -63.7
244.0 10649 -48.9 -63.9
243.3 10668 -48.9 -63.9
220.0 11327 -50.3 -65.3
212.0 11569 -50.5 -65.5
210.0 11631 -49.7 -64.7
200.0 11950 -49.9 -64.9
194.0 12149 -49.9 -64.9
183.0 12529 -51.3 -66.3
164.0 13233 -55.3 -68.3
152.0 13716 -56.5 -69.5
150.0 13800 -57.1 -70.1
136.0 14414 -60.5 -72.5
132.0 14600 -60.1 -72.1
131.4 14630 -60.2 -72.2
128.0 14792 -60.9 -72.9
125.0 14939 -60.1 -72.1
119.0 15240 -62.2 -73.8
112.0 15616 -64.9 -75.9
108.0 15838 -64.1 -75.1
107.8 15850 -64.1 -75.1
105.0 16010 -64.7 -75.7
103.0 16128 -62.9 -73.9
100.0 16310 -62.5 -73.5
'''
# Parse the data
sound_data = StringIO(data_txt)
p, h, T, Td = np.loadtxt(sound_data, unpack=True)
# Create a new figure. The dimensions here give a good aspect ratio
fig = plt.figure(figsize=(6.5875, 6.2125))
ax = fig.add_subplot(projection='skewx')
plt.grid(True)
# Plot the data using normal plotting functions, in this case using
# log scaling in Y, as dictated by the typical meteorological plot
ax.semilogy(T, p, color='C3')
ax.semilogy(Td, p, color='C2')
# An example of a slanted line at constant X
l = ax.axvline(0, color='C0')
# Disables the log-formatting that comes with semilogy
ax.yaxis.set_major_formatter(ScalarFormatter())
ax.yaxis.set_minor_formatter(NullFormatter())
ax.set_yticks(np.linspace(100, 1000, 10))
ax.set_ylim(1050, 100)
ax.xaxis.set_major_locator(MultipleLocator(10))
ax.set_xlim(-50, 50)
plt.show()
参考
本示例展示了以下函数、方法、类和模块的使用