注意
跳转到末尾以下载完整示例代码。
变换教程#
与任何图形包一样,Matplotlib 构建于一个变换框架之上,以便在坐标系之间轻松移动:用户层面的数据坐标系、坐标轴坐标系、图坐标系和显示坐标系。在 95% 的绘图场景中,你无需考虑这一点,因为它在幕后发生,但当你突破自定义图表生成的限制时,理解这些对象会很有帮助,这样你就可以重用 Matplotlib 提供给你的现有变换,或创建自己的变换(参见 matplotlib.transforms)。下表总结了一些有用的坐标系、每个系统的描述以及从每个坐标系到显示坐标系的变换对象。在“变换对象”列中,ax 是一个 Axes 实例,fig 是一个 Figure 实例,而 subfigure 是一个 SubFigure 实例。
坐标系 |
描述 |
从系统到显示的变换对象 |
|---|---|---|
数据 |
坐标轴中数据的坐标系。 |
|
坐标轴 |
|
|
子图 |
|
|
图 |
|
|
图-英寸 |
|
|
x轴, y轴 |
混合坐标系,在一个方向上使用数据坐标,在另一个方向上使用坐标轴坐标。 |
|
显示 |
输出的原生坐标系;(0, 0) 是窗口的左下角,(宽度, 高度) 是输出的右上角(以“显示单位”表示)。 单位的确切解释取决于后端。例如,对于 Agg 是像素,对于 svg/pdf 是点。 |
Transform 对象对源和目标坐标系是无感知的,然而,上表中提到的对象被构造为在其自己的坐标系中接收输入,并将输入变换到显示坐标系。这就是为什么显示坐标系的“变换对象”列为 None ——因为它本身就处于显示坐标系中。命名和目标约定有助于跟踪可用的“标准”坐标系和变换。
这些变换还知道如何反转自身(通过 Transform.inverted)以生成从输出坐标系返回到输入坐标系的变换。例如,ax.transData 将数据坐标中的值转换为显示坐标,而 ax.transData.inverted() 是一个从显示坐标到数据坐标的 matplotlib.transforms.Transform。这在处理用户界面事件时特别有用,因为这些事件通常发生在显示空间中,而你希望知道鼠标点击或按键在你的数据坐标系中的位置。
请注意,如果在显示坐标系中指定 Artist 的位置,当 dpi 或图的大小改变时,它们的相对位置可能会发生变化。这在打印或改变屏幕分辨率时可能导致混淆,因为对象的位置和大小都会改变。因此,对于放置在 Axes 或图中的 Artist,通常将其变换设置为除了 IdentityTransform() 之外的其他变换;当使用 add_artist 将 Artist 添加到 Axes 时,默认的变换是 ax.transData,这样你就可以在数据坐标系中工作和思考,而让 Matplotlib 处理到显示坐标系的变换。
数据坐标#
让我们从最常用的坐标系——数据坐标系开始。每当你向 Axes 添加数据时,Matplotlib 都会更新数据限制,最常用 set_xlim() 和 set_ylim() 方法进行更新。例如,在下图中,数据限制在 x 轴上从 0 延伸到 10,在 y 轴上从 -1 延伸到 1。
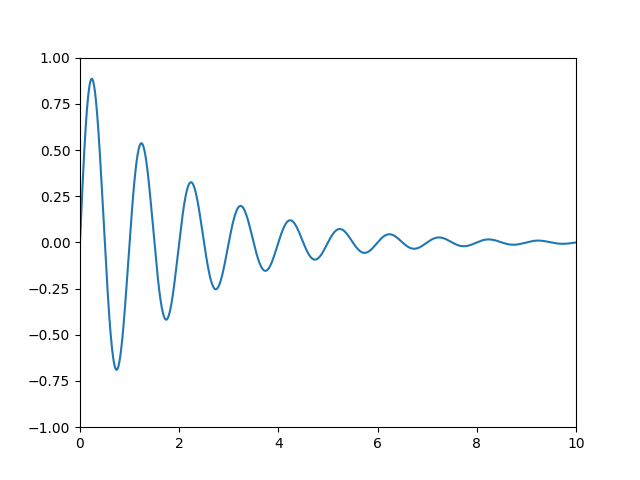
你可以使用 ax.transData 实例将你的数据转换为显示坐标系,可以是单个点或一系列点,如下所示
In [14]: type(ax.transData)
Out[14]: <class 'matplotlib.transforms.CompositeGenericTransform'>
In [15]: ax.transData.transform((5, 0))
Out[15]: array([ 335.175, 247. ])
In [16]: ax.transData.transform([(5, 0), (1, 2)])
Out[16]:
array([[ 335.175, 247. ],
[ 132.435, 642.2 ]])
你可以使用 inverted() 方法来创建一个变换,它将你从显示坐标系带到数据坐标系
In [41]: inv = ax.transData.inverted()
In [42]: type(inv)
Out[42]: <class 'matplotlib.transforms.CompositeGenericTransform'>
In [43]: inv.transform((335.175, 247.))
Out[43]: array([ 5., 0.])
如果你跟着本教程一起敲代码,如果你有不同的窗口大小或 dpi 设置,显示坐标的精确值可能会有所不同。同样,在下图中,显示标签点的数值可能与 ipython 会话中的不同,因为文档图的大小默认值是不同的。
x = np.arange(0, 10, 0.005)
y = np.exp(-x/2.) * np.sin(2*np.pi*x)
fig, ax = plt.subplots()
ax.plot(x, y)
ax.set_xlim(0, 10)
ax.set_ylim(-1, 1)
xdata, ydata = 5, 0
# This computing the transform now, if anything
# (figure size, dpi, axes placement, data limits, scales..)
# changes re-calling transform will get a different value.
xdisplay, ydisplay = ax.transData.transform((xdata, ydata))
bbox = dict(boxstyle="round", fc="0.8")
arrowprops = dict(
arrowstyle="->",
connectionstyle="angle,angleA=0,angleB=90,rad=10")
offset = 72
ax.annotate(f'data = ({xdata:.1f}, {ydata:.1f})',
(xdata, ydata), xytext=(-2*offset, offset), textcoords='offset points',
bbox=bbox, arrowprops=arrowprops)
disp = ax.annotate(f'display = ({xdisplay:.1f}, {ydisplay:.1f})',
(xdisplay, ydisplay), xytext=(0.5*offset, -offset),
xycoords='figure pixels',
textcoords='offset points',
bbox=bbox, arrowprops=arrowprops)
plt.show()
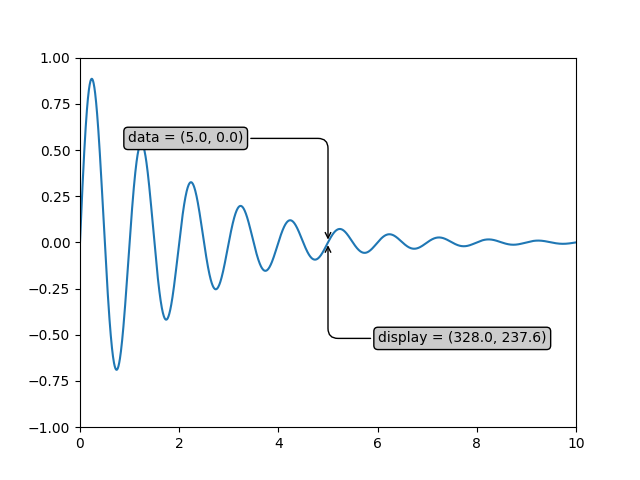
警告
如果你在 GUI 后端运行上述示例中的源代码,你可能还会发现数据和显示注释的两个箭头不完全指向同一点。这是因为显示点是在图显示之前计算的,而 GUI 后端在创建图时可能会稍微调整图的大小。如果你自己调整图的大小,这种效果会更明显。这是你很少想在显示空间中工作的一个好原因,但你可以连接到 'on_draw' Event,以便在图绘制时更新图坐标;参见 事件处理和拾取。
当你改变坐标轴的 x 或 y 限制时,数据限制会随之更新,从而使变换产生一个新的显示点。请注意,当我们只改变 ylim 时,只有 y-显示坐标会改变,而当我们也改变 xlim 时,两者都会改变。稍后当我们讨论 Bbox 时,会对此进行更多说明。
In [54]: ax.transData.transform((5, 0))
Out[54]: array([ 335.175, 247. ])
In [55]: ax.set_ylim(-1, 2)
Out[55]: (-1, 2)
In [56]: ax.transData.transform((5, 0))
Out[56]: array([ 335.175 , 181.13333333])
In [57]: ax.set_xlim(10, 20)
Out[57]: (10, 20)
In [58]: ax.transData.transform((5, 0))
Out[58]: array([-171.675 , 181.13333333])
坐标轴坐标#
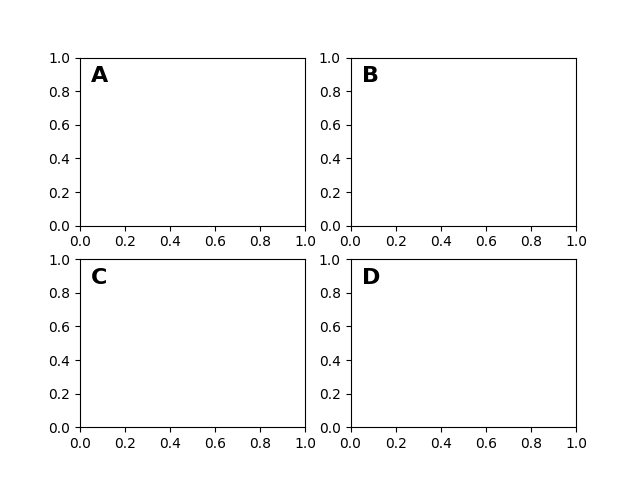
在数据坐标系之后,坐标轴坐标系可能是第二个最有用的坐标系。在这里,点 (0, 0) 是你的 Axes 或子图的左下角,(0.5, 0.5) 是中心,(1.0, 1.0) 是右上角。你也可以引用范围之外的点,所以 (-0.1, 1.1) 位于你的 Axes 的左侧和上方。这个坐标系在你的 Axes 中放置文本时非常有用,因为你通常希望文本气泡位于固定位置,例如 Axes 面板的左上角,并且当你平移或缩放时,该位置保持固定。这是一个简单的例子,它创建了四个面板并将其标记为 'A'、'B'、'C'、'D',正如你在期刊中经常看到的那样。有关此类标签的更复杂方法,请参见 子图标签。
fig = plt.figure()
for i, label in enumerate(('A', 'B', 'C', 'D')):
ax = fig.add_subplot(2, 2, i+1)
ax.text(0.05, 0.95, label, transform=ax.transAxes,
fontsize=16, fontweight='bold', va='top')
plt.show()
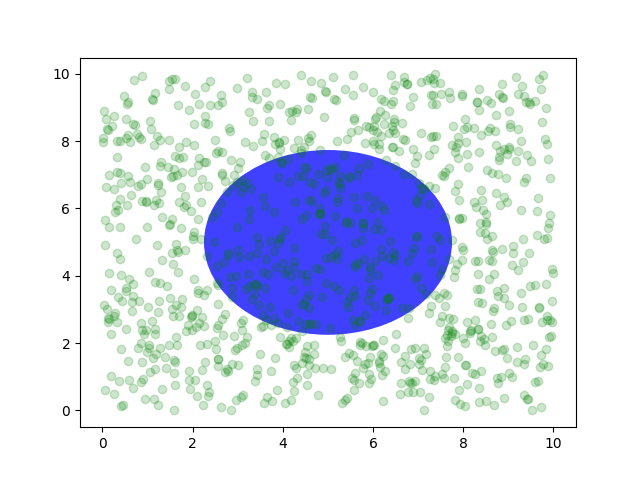
你也可以在坐标轴坐标系中绘制线或补丁,但根据我的经验,这不如使用 ax.transAxes 来放置文本有用。尽管如此,这里有一个有趣的例子,它在数据空间中绘制了一些随机点,并覆盖了一个半透明的 Circle,其中心位于 Axes 的中央,半径是 Axes 的四分之一——如果你的 Axes 不保留宽高比(参见 set_aspect()),这看起来就像一个椭圆。使用平移/缩放工具移动,或者手动改变数据的 xlim 和 ylim,你会看到数据移动,但圆圈将保持固定,因为它不在数据坐标系中,并且将始终保持在 Axes 的中心。
fig, ax = plt.subplots()
x, y = 10*np.random.rand(2, 1000)
ax.plot(x, y, 'go', alpha=0.2) # plot some data in data coordinates
circ = mpatches.Circle((0.5, 0.5), 0.25, transform=ax.transAxes,
facecolor='blue', alpha=0.75)
ax.add_patch(circ)
plt.show()
混合变换#
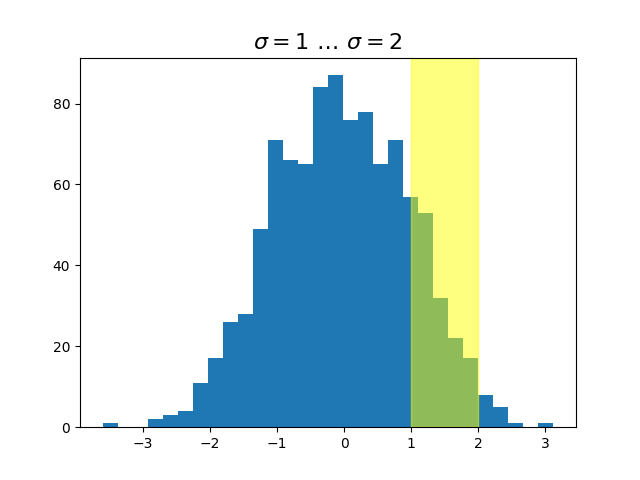
在混合坐标轴和数据坐标的混合坐标空间中绘图非常有用,例如创建水平跨度以突出显示 y 数据的一部分区域,但无论数据限制、平移或缩放级别如何,都横跨 x 轴。事实上,这些混合线和跨度非常有用,我们有内置函数可以轻松绘制它们(参见 axhline(), axvline(), axhspan(), axvspan()),但出于教学目的,我们将在此处使用混合变换实现水平跨度。这个技巧只适用于可分离变换,就像你在正常笛卡尔坐标系中看到的那样,而不适用于不可分离变换,例如 PolarTransform。
import matplotlib.transforms as transforms
fig, ax = plt.subplots()
x = np.random.randn(1000)
ax.hist(x, 30)
ax.set_title(r'$\sigma=1 \/ \dots \/ \sigma=2$', fontsize=16)
# the x coords of this transformation are data, and the y coord are axes
trans = transforms.blended_transform_factory(
ax.transData, ax.transAxes)
# highlight the 1..2 stddev region with a span.
# We want x to be in data coordinates and y to span from 0..1 in axes coords.
rect = mpatches.Rectangle((1, 0), width=1, height=1, transform=trans,
color='yellow', alpha=0.5)
ax.add_patch(rect)
plt.show()
注意
当 x 位于数据坐标系,y 位于坐标轴坐标系时的混合变换非常有用,以至于我们有辅助方法来返回 Matplotlib 内部用于绘制刻度、刻度标签等的版本。这些方法是 matplotlib.axes.Axes.get_xaxis_transform() 和 matplotlib.axes.Axes.get_yaxis_transform()。因此,在上面的例子中,对 blended_transform_factory() 的调用可以替换为 get_xaxis_transform
在物理坐标系中绘图#
有时我们希望对象在图上具有特定的物理尺寸。这里我们绘制与上面相同的圆,但使用物理坐标。如果以交互方式进行,你会看到改变图的大小不会改变圆与左下角的偏移,也不会改变其大小,并且无论 Axes 的宽高比如何,圆都保持为圆。
fig, ax = plt.subplots(figsize=(5, 4))
x, y = 10*np.random.rand(2, 1000)
ax.plot(x, y*10., 'go', alpha=0.2) # plot some data in data coordinates
# add a circle in fixed-coordinates
circ = mpatches.Circle((2.5, 2), 1.0, transform=fig.dpi_scale_trans,
facecolor='blue', alpha=0.75)
ax.add_patch(circ)
plt.show()
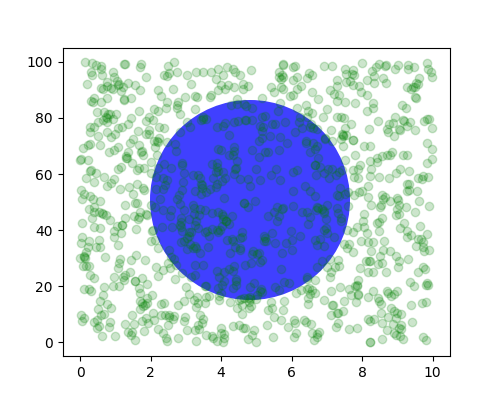
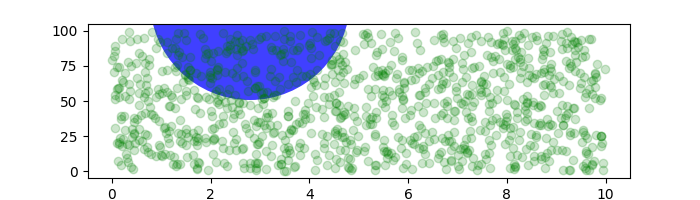
如果我们改变图的大小,圆圈不会改变其绝对位置,并且会被裁剪。
fig, ax = plt.subplots(figsize=(7, 2))
x, y = 10*np.random.rand(2, 1000)
ax.plot(x, y*10., 'go', alpha=0.2) # plot some data in data coordinates
# add a circle in fixed-coordinates
circ = mpatches.Circle((2.5, 2), 1.0, transform=fig.dpi_scale_trans,
facecolor='blue', alpha=0.75)
ax.add_patch(circ)
plt.show()
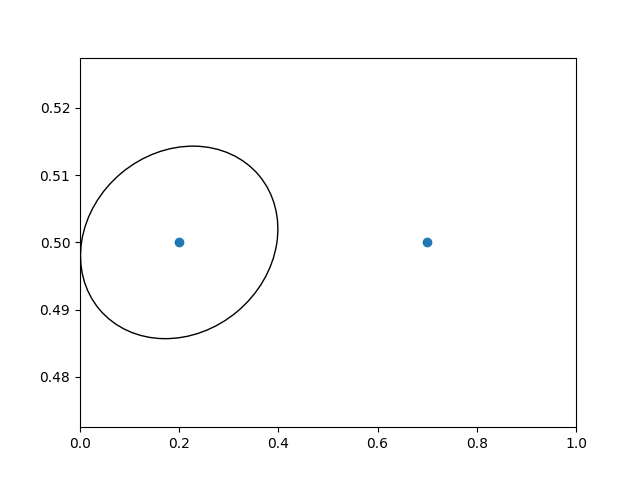
另一个用途是在 Axes 上围绕数据点放置具有设定物理尺寸的补丁。这里我们将两个变换组合起来。第一个设置椭圆的大小缩放,第二个设置其位置。然后,椭圆被放置在原点,接着我们使用辅助变换 ScaledTranslation 将其移动到 ax.transData 坐标系中的正确位置。这个辅助类通过以下方式实例化:
trans = ScaledTranslation(xt, yt, scale_trans)
其中 xt 和 yt 是平移偏移量,scale_trans 是一个在应用偏移量之前在变换时缩放 xt 和 yt 的变换。
请注意下面变换中加号运算符的使用。这段代码表示:首先应用缩放变换 fig.dpi_scale_trans,使椭圆具有适当的大小,但仍以 (0, 0) 为中心,然后将数据平移到数据空间中的 xdata[0] 和 ydata[0]。
在交互使用中,即使通过缩放改变了坐标轴限制,椭圆的大小也保持不变。
fig, ax = plt.subplots()
xdata, ydata = (0.2, 0.7), (0.5, 0.5)
ax.plot(xdata, ydata, "o")
ax.set_xlim((0, 1))
trans = (fig.dpi_scale_trans +
transforms.ScaledTranslation(xdata[0], ydata[0], ax.transData))
# plot an ellipse around the point that is 150 x 130 points in diameter...
circle = mpatches.Ellipse((0, 0), 150/72, 130/72, angle=40,
fill=None, transform=trans)
ax.add_patch(circle)
plt.show()
注意
变换的顺序很重要。这里椭圆首先在显示空间中获得正确的尺寸,然后才在数据空间中移动到正确的位置。如果我先执行 ScaledTranslation,那么 xdata[0] 和 ydata[0] 将首先被转换为显示坐标(在 200 dpi 显示器上是 [ 358.4 475.2]),然后这些坐标会由 fig.dpi_scale_trans 进行缩放,从而将椭圆的中心推离屏幕很远(即 [ 71680. 95040.])。
使用偏移变换创建阴影效果#
ScaledTranslation 的另一个用途是创建一个与另一个变换有偏移的新变换,例如,将一个对象相对于另一个对象稍微平移。通常,你希望平移以某种物理尺寸(如点或英寸)进行,而不是以数据坐标进行,这样在不同的缩放级别和 dpi 设置下,平移效果保持不变。
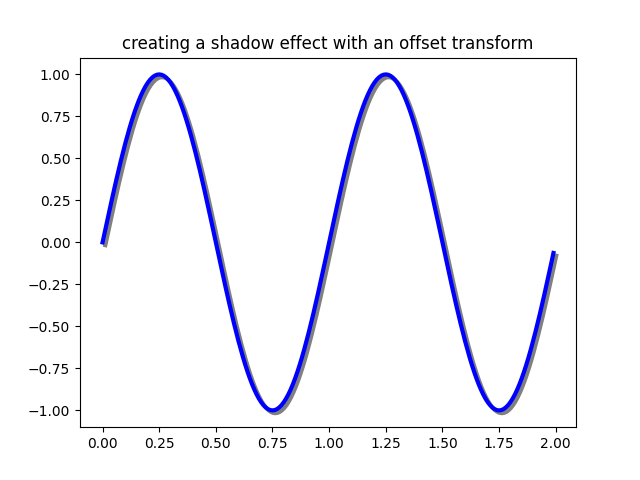
偏移的一个用途是创建阴影效果,你可以绘制一个与第一个对象相同但稍微向右和下方偏移的对象,调整 zorder 以确保阴影首先绘制,然后在其上方绘制被阴影覆盖的对象。
这里我们应用变换的顺序与上面使用 ScaledTranslation 的顺序相反。绘图首先在数据坐标系 (ax.transData) 中完成,然后使用 fig.dpi_scale_trans 偏移 dx 和 dy 个点。(在排版中,一个点是 1/72 英寸,通过以点为单位指定偏移量,无论图以何种 dpi 分辨率保存,其外观都将保持一致。)
fig, ax = plt.subplots()
# make a simple sine wave
x = np.arange(0., 2., 0.01)
y = np.sin(2*np.pi*x)
line, = ax.plot(x, y, lw=3, color='blue')
# shift the object over 2 points, and down 2 points
dx, dy = 2/72., -2/72.
offset = transforms.ScaledTranslation(dx, dy, fig.dpi_scale_trans)
shadow_transform = ax.transData + offset
# now plot the same data with our offset transform;
# use the zorder to make sure we are below the line
ax.plot(x, y, lw=3, color='gray',
transform=shadow_transform,
zorder=0.5*line.get_zorder())
ax.set_title('creating a shadow effect with an offset transform')
plt.show()
注意
dpi 和英寸偏移是一个足够常见的用例,我们有一个特殊的辅助函数来在 matplotlib.transforms.offset_copy() 中创建它,该函数返回一个带有额外偏移的新变换。因此,在上面我们可以这样做:
shadow_transform = transforms.offset_copy(ax.transData,
fig, dx, dy, units='inches')
变换管道#
本教程中我们一直使用的 ax.transData 变换是由三个不同变换组成的复合变换,它们构成了从数据到显示坐标的变换管道。Michael Droettboom 实现了变换框架,并注意提供一个清晰的 API,将极坐标和对数图中发生的非线性投影和缩放与平移和缩放时发生的线性仿射变换分开。这里存在效率优势,因为你可以在 Axes 中平移和缩放,这会影响仿射变换,但对于简单的导航事件,你可能无需计算潜在昂贵的非线性缩放或投影。还可以将仿射变换矩阵相乘,然后一步将其应用于坐标。并非所有可能的变换都如此。
以下是 ax.transData 实例在基本可分离的坐标轴 Axes 类中定义的方式:
self.transData = self.transScale + (self.transLimits + self.transAxes)
我们已经在上面 坐标轴坐标 中介绍了 transAxes 实例,它将 Axes 或子图边界框的 (0, 0)、(1, 1) 角映射到显示空间,所以我们来看看另外两个部分。
self.transLimits 是将你从数据坐标系转换到坐标轴坐标系的变换;也就是说,它将你的视图 xlim 和 ylim 映射到 Axes 的单位空间(然后 transAxes 将该单位空间转换到显示空间)。我们可以在这里看到它的作用:
In [80]: ax = plt.subplot()
In [81]: ax.set_xlim(0, 10)
Out[81]: (0, 10)
In [82]: ax.set_ylim(-1, 1)
Out[82]: (-1, 1)
In [84]: ax.transLimits.transform((0, -1))
Out[84]: array([ 0., 0.])
In [85]: ax.transLimits.transform((10, -1))
Out[85]: array([ 1., 0.])
In [86]: ax.transLimits.transform((10, 1))
Out[86]: array([ 1., 1.])
In [87]: ax.transLimits.transform((5, 0))
Out[87]: array([ 0.5, 0.5])
我们可以使用这个相同的反向变换从单位坐标轴坐标系回到数据坐标系。
In [90]: inv.transform((0.25, 0.25))
Out[90]: array([ 2.5, -0.5])
最后一部分是 self.transScale 属性,它负责数据的可选非线性缩放,例如,用于对数坐标轴。当 Axes 初次设置时,它被设置为恒等变换,因为基本的 Matplotlib 坐标轴具有线性刻度,但当你调用像 semilogx() 这样的对数缩放函数,或者使用 set_xscale() 明确将刻度设置为对数时,ax.transScale 属性就会被设置为处理非线性投影。这些刻度变换是各自 xaxis 和 yaxis Axis 实例的属性。例如,当你调用 ax.set_xscale('log') 时,xaxis 会将其刻度更新为 matplotlib.scale.LogScale 实例。
对于非可分离的坐标轴,如 PolarAxes,还需要考虑一个部分,即投影变换。transData matplotlib.projections.polar.PolarAxes 与典型的可分离 Matplotlib Axes 相似,但多了一个 transProjection 部分:
self.transData = (
self.transScale + self.transShift + self.transProjection +
(self.transProjectionAffine + self.transWedge + self.transAxes))
transProjection 处理从特定空间(例如,地图数据的纬度和经度,或极坐标数据的半径和角度)到可分离笛卡尔坐标系的投影。在 matplotlib.projections 包中,有几个投影示例,了解更多信息最好是打开这些包的源代码,看看如何创建自己的投影,因为 Matplotlib 支持可扩展的坐标轴和投影。Michael Droettboom 提供了一个创建 Hammer 投影坐标轴的优秀教程示例;参见 自定义投影。
脚本总运行时间: (0 分钟 3.001 秒)